During the last two days, we reviewed all the features learned during the first five days of the Practical symfony book to customize Jobeet features and add new ones. In the process, we have also touched on other more advanced symfony features.
Today, we will start talking about something completely different: automated tests. As the topic is quite large, it will take us two full days to cover everything.
Tests in symfony
There are two different kinds of automated tests in symfony: unit tests|Unit Testing and functional tests.
Unit tests verify that each method and function is working properly. Each test must be as independent as possible from the others.
On the other hand, functional tests verify that the resulting application behaves correctly as a whole.
All tests in symfony are located under the test/ directory of the project. It
contains two sub-directories, one for unit tests (test/unit/) and one for
functional tests (test/functional/).
Unit tests will be covered today, whereas tomorrow will be dedicated to functional tests.
Unit Tests
Writing unit tests is perhaps one of the hardest web development best practices to put into action. As web developers are not really used to testing their work, a lot of questions arise: Do I have to write tests before implementing a feature? What do I need to test? Do my tests need to cover every single edge case|Edge Cases? How can I be sure that everything is well tested? But usually, the first question is much more basic: Where to start?
Even if we strongly advocate testing, the symfony approach is pragmatic: it's always better to have some tests than no test at all. Do you already have a lot of code without any test? No problem. You don't need to have a full test suite to benefit from the advantages of having tests. Start by adding tests whenever you find a bug in your code. Over time, your code will become better, the code coverage|Code Coverage will rise, and you will become more confident about it. By starting with a pragmatic approach, you will feel more comfortable with tests over time. The next step is to write tests for new features. In no time, you will become a test addict.
The problem with most testing libraries is their steep learning curve. That's why symfony provides a very simple testing library, lime, to make writing test insanely easy.
note
Even if this tutorial describes the lime built-in library extensively, you can use any testing library, like the excellent PHPUnit library.
The lime Testing Framework
All unit tests written with the lime framework start with the same code:
require_once dirname(__FILE__).'/../bootstrap/unit.php'; $t = new lime_test(1);
First, the unit.php bootstrap file is included to initialize a few things.
Then, a new lime_test object is created and the number of tests planned to be
launched is passed as an argument.
note
The plan allows lime to output an error message in case too few tests are run (for instance when a test generates a PHP fatal error).
Testing works by calling a method or a function with a set of predefined inputs and then comparing the results with the expected output. This comparison determines whether a test passes or fails.
To ease the comparison, the lime_test object provides several methods:
| Method | Description |
|---|---|
ok($test) |
Tests a condition and passes if it is true |
is($value1, $value2) |
Compares two values and passes if they are |
equal (==) |
|
isnt($value1, $value2) |
Compares two values and passes if they are |
| not equal | |
like($string, $regexp) |
Tests a string against a regular expression |
unlike($string, $regexp) |
Checks that a string doesn't match a regular |
| expression | |
is_deeply($array1, $array2) |
Checks that two arrays have the same values |
tip
You may wonder why lime defines so many test methods, as all tests can be
written just by using the ok() method. The benefit of alternative methods
lies in much more explicit error messages in case of a failed test and in
improved readability of the tests.
The lime_test object also provides other convenient testing methods:
| Method | Description |
|---|---|
fail() |
Always fails--useful for testing exceptions |
pass() |
Always passes--useful for testing exceptions |
skip($msg, $nb_tests) |
Counts as $nb_tests tests--useful for conditional |
| tests | |
todo() |
Counts as a test--useful for tests yet to be |
| written |
Finally, the comment($msg) method outputs a comment but runs no test.
Running Unit Tests
All unit tests are stored under the test/unit/ directory. By convention, tests
are named after the class they test and suffixed by Test. Although you can
organize the files under the test/unit/ directory anyway you like, we
recommend you replicate the directory structure of the lib/ directory.
To illustrate unit testing, we will test the Jobeet class.
Create a test/unit/JobeetTest.php file and copy the following code inside:
// test/unit/JobeetTest.php require_once dirname(__FILE__).'/../bootstrap/unit.php'; $t = new lime_test(1); $t->pass('This test always passes.');
To launch the tests, you can execute the file directly:
$ php test/unit/JobeetTest.php
Or use the test:unit task:
$ php symfony test:unit Jobeet

note
Windows command line unfortunately cannot highlight test results in
red or green color. But if you use Cygwin, you can force symfony to use
colors by passing the --color option to the task.
Testing slugify
Let's start our trip to the wonderful world of unit testing by writing tests for
the Jobeet::slugify() method.
We created the ~slug|Slug~ify() method during day 5 to clean up a string
so that it can be safely included in a URL. The conversion consists in some
basic transformations like converting all non-ASCII characters to a dash (-)
or converting the string to lowercase:
| Input | Output |
|---|---|
| Sensio Labs | sensio-labs |
| Paris, France | paris-france |
Replace the content of the test file with the following code:
// test/unit/JobeetTest.php require_once dirname(__FILE__).'/../bootstrap/unit.php'; $t = new lime_test(6); $t->is(Jobeet::slugify('Sensio'), 'sensio'); $t->is(Jobeet::slugify('sensio labs'), 'sensio-labs'); $t->is(Jobeet::slugify('sensio labs'), 'sensio-labs'); $t->is(Jobeet::slugify('paris,france'), 'paris-france'); $t->is(Jobeet::slugify(' sensio'), 'sensio'); $t->is(Jobeet::slugify('sensio '), 'sensio');
If you take a closer look at the tests we have written, you will notice that each line only tests one thing. That's something you need to keep in mind when writing unit tests. Test one thing at a time.
You can now execute the test file. If all tests pass, as we expect them to, you will enjoy the "green bar". If not, the infamous "red bar" will alert you that some tests do not pass and that you need to fix them.
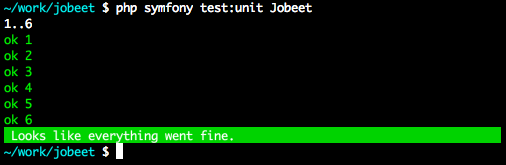
If a test fails, the output will give you some information about why it failed; but if you have hundreds of tests in a file, it can be difficult to quickly identify the behavior that fails.
All lime test methods take a string as their last argument that serves as the
description for the test. It's very convenient as it forces you to describe what
you are really testing. It can also serve as a form of
documentation for a method's expected behavior. Let's add some
messages to the slugify test file:
require_once dirname(__FILE__).'/../bootstrap/unit.php'; $t = new lime_test(6); $t->comment('::slugify()'); $t->is(Jobeet::slugify('Sensio'), 'sensio', '::slugify() converts all characters to lower case'); $t->is(Jobeet::slugify('sensio labs'), 'sensio-labs', '::slugify() replaces a white space by a -'); $t->is(Jobeet::slugify('sensio labs'), 'sensio-labs', '::slugify() replaces several white spaces by a single -'); $t->is(Jobeet::slugify(' sensio'), 'sensio', '::slugify() removes - at the beginning of a string'); $t->is(Jobeet::slugify('sensio '), 'sensio', '::slugify() removes - at the end of a string'); $t->is(Jobeet::slugify('paris,france'), 'paris-france', '::slugify() replaces non-ASCII characters by a -');
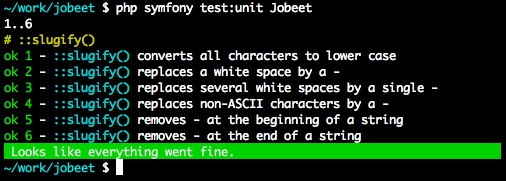
The test description string is also a valuable tool when trying to figure out what to test. You can see a pattern in the test strings: they are sentences describing how the method must behave and they always start with the method name to test.
Adding Tests for new Features
The slug for an empty string is an empty string. You can test it, it will work.
But an empty string in a URL is not that a great idea. Let's change the
slugify() method so that it returns the "n-a" string in case of an empty
string.
You can write the test first, then update the method, or the other way around. It is really a matter of taste but writing the test first gives you the confidence that your code actually implements what you planned:
$t->is(Jobeet::slugify(''), 'n-a', '::slugify() converts the empty string to n-a');
This development methodology, where you first write tests then implement features, is known as Test Driven Development (TDD).
If you launch the tests now, you must have a red bar. If not, it means that the feature is already implemented or that your test does not test what it is supposed to test.
Now, edit the Jobeet class and add the following condition at the beginning:
// lib/Jobeet.class.php static public function slugify($text) { if (empty($text)) { return 'n-a'; } // ... }
The test must now pass as expected, and you can enjoy the green bar, but only if you have remembered to update the test plan. If not, you will have a message that says you planned six tests and ran one extra. Having the planned test count up to date is important, as it you will keep you informed if the test script dies early on.
Adding Tests because of a Bug
Let's say that time has passed and one of your users reports a weird bug: some job links point to a 404 error page. After some investigation, you find that for some reason, these jobs have an empty company, position, or location slug.
How is it possible?
You look through the records in the database and the columns are definitely not
empty. You think about it for a while, and bingo, you find the cause. When a
string only contains non-ASCII characters, the slugify() method converts it to
an empty string. So happy to have found the cause, you open the Jobeet class
and fix the problem right away. That's a bad idea. First, let's add a test:
$t->is(Jobeet::slugify(' - '), 'n-a', '::slugify() converts a string that only contains non-ASCII characters to n-a');
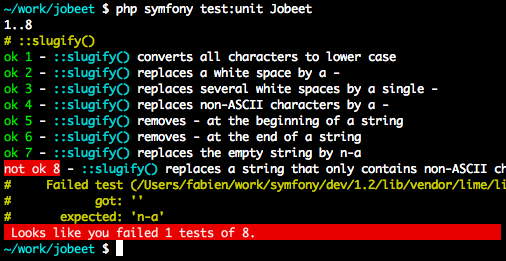
After checking that the test does not pass, edit the Jobeet class and move the
empty string check to the end of the method:
static public function slugify($text) { // ... if (empty($text)) { return 'n-a'; } return $text; }
The new test now passes, as do all the other ones. The slugify() had a bug
despite our 100% coverage.
You cannot think about all edge cases when writing tests, and that's fine. But when you discover one, you need to write a test for it before fixing your code. It also means that your code will get better over time, which is always a good thing.
Propel Unit Tests
Database Configuration
Unit testing a Propel model class is a bit more complex as it requires a database connection. You already have the one you use for your development, but it is a good habit to create a dedicated database for tests.
At the beginning of this book, we introduced the environments as
a way to vary an application's settings. By default, all symfony tests are run
in the test environment, so let's configure a different database for the
test environment:
$ php symfony configure:database --env=test "mysql:host=localhost;dbname=jobeet_test" root mYsEcret
The env option tells the task that the database configuration is only for the
test environment. When we used this task during day 3, we did not pass any
env option, so the configuration was applied to all environments.
note
If you are curious, open the config/databases.yml configuration file to see
how symfony makes it easy to change the configuration depending on the
environment.
Now that we have configured the database, we can bootstrap it by using the
propel:insert-sql task:
$ mysqladmin -uroot -pmYsEcret create jobeet_test $ php symfony propel:insert-sql --env=test
Test Data
Now that we have a dedicated database for our tests, we need a way to load some
test data. During day 3, you learned to use the propel:data-load
task, but for tests, we need to reload the data each time we run them to
put the database in a known state.
The propel:data-load task internally uses the
sfPropelData class to
load the data:
$loader = new sfPropelData(); $loader->loadData(sfConfig::get('sf_test_dir').'/fixtures');
note
The sfConfig object can be used to get the full path of a project
sub-directory. Using it allows for the default directory structure to be
customized.
The loadData() method takes a directory or a file as its first argument. It
can also take an array of directories and/or files.
We have already created some initial data in the data/fixtures/ directory. For
tests, we will put the fixtures into the test/fixtures/ directory.
These fixtures will be used for Propel unit and functional tests.
For now, copy the files from data/fixtures/ to the test/fixtures/ directory.
Testing JobeetJob
Let's create some unit tests for the JobeetJob model class.
As all our Propel unit tests will begin with the same code, create a
Propel.php file in the bootstrap/ test directory with the following code:
// test/bootstrap/Propel.php include(dirname(__FILE__).'/unit.php'); $configuration = ProjectConfiguration::getApplicationConfiguration( 'frontend', 'test', true); new sfDatabaseManager($configuration); $loader = new sfPropelData(); $loader->loadData(sfConfig::get('sf_test_dir').'/fixtures');
The script is pretty self-explanatory:
As for the front controllers, we initialize a configuration object for the
testenvironment:$configuration = ProjectConfiguration::getApplicationConfiguration( 'frontend', 'test', true);
We create a database manager. It initializes the Propel connection by loading the
databases.ymlconfiguration file.new sfDatabaseManager($configuration);
We load our test data by using
sfPropelData:$loader = new sfPropelData(); $loader->loadData(sfConfig::get('sf_test_dir').'/fixtures');
note
Propel connects to the database only if it has some SQL statements to execute.
Now that everything is in place, we can start testing the JobeetJob class.
First, we need to create the JobeetJobTest.php file in test/unit/model:
// test/unit/model/JobeetJobTest.php include(dirname(__FILE__).'/../../bootstrap/Propel.php'); $t = new lime_test(1);
Then, let's start by adding a test for the getCompanySlug() method:
$t->comment('->getCompanySlug()'); $job = JobeetJobPeer::doSelectOne(new Criteria()); $t->is($job->getCompanySlug(), Jobeet::slugify($job->getCompany()), '->getCompanySlug() return the slug for the company');
Notice that we only test the getCompanySlug() method and not if the slug is
correct or not, as we are already testing this elsewhere.
Writing tests for the save() method is slightly more complex:
$t->comment('->save()'); $job = create_job(); $job->save(); $expiresAt = date('Y-m-d', time() + 86400 * sfConfig::get('app_active_days')); $t->is($job->getExpiresAt('Y-m-d'), $expiresAt, '->save() updates expires_at if not set'); $job = create_job(array('expires_at' => '2008-08-08')); $job->save(); $t->is($job->getExpiresAt('Y-m-d'), '2008-08-08', '->save() does not update expires_at if set'); function create_job($defaults = array()) { static $category = null; if (is_null($category)) { $category = JobeetCategoryPeer::doSelectOne(new Criteria()); } $job = new JobeetJob(); $job->fromArray(array_merge(array( 'category_id' => $category->getId(), 'company' => 'Sensio Labs', 'position' => 'Senior Tester', 'location' => 'Paris, France', 'description' => 'Testing is fun', 'how_to_apply' => 'Send e-Mail', 'email' => 'job@example.com', 'token' => rand(1111, 9999), 'is_activated' => true, ), $defaults), BasePeer::TYPE_FIELDNAME); return $job; }
note
Each time you add tests, don't forget to update the number of expected tests
(the plan) in the lime_test constructor method. For the JobeetJobTest
file, you need to change it from 1 to 3.
Test other Propel Classes
You can now add tests for all other Propel classes. As you are now getting used to the process of writing unit tests, it should be quite easy.
Unit Tests Harness
The test:unit task can also be used to launch all unit tests for a
project:
$ php symfony test:unit
The task outputs whether each test file passes or fails:

tip
If the test:unit task returns a "dubious status" for a
file, it indicates that the script died before end. Running the test file
alone will give you the exact error message.
Final Thoughts
Even if testing an application is quite important, I know that some of you might have been tempted to just skip this day. I'm glad you have not.
Sure, embracing symfony is about learning all the great features the framework provides, but it's also about its philosophy of development and the best practices it advocates. And testing is one of them. Sooner or later, unit tests will save the day for you. They give you a solid confidence about your code and the freedom to refactor it without fear. Unit tests are a safe guard that will alert you if you break something. The symfony framework itself has more than 9000 tests.
Tomorrow, we will write some functional tests for the job and category
modules. Until then, take some time to write more unit tests for the Jobeet
model classes.
This work is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported License license.